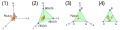
English: Derivation of a ternary plot from Cartesian coordinates:
Figure (1) shows an oblique projection of point P(a,b,c) in a 3-dimensional Cartesian space with axes a, b and c, respectively.
If a + b + c = K (a positive constant), P is restricted to a plane containing A(K,0,0), B(0,K,0) and C(0,0,K). If a, b and c each cannot be negative, P is restricted to the triangle bounded by A, B and C, as in (2).
In (3), the axes are rotated to give an isometric view. The triangle, viewed face-on, appears equilateral.
In (4), the distances of P from lines BC, AC and AB are denoted by a' , b' and c' , respectively.
For any line l = s + t n̂ in vector form (n̂ is a unit vector) and a point p, the distance from a point to a line from p to l is  .
.
In this case, point P is at
 .
.
Line BC has
 and
and
 .
.
Using the perpendicular distance formula,

Substituting K = a + b + c,
 .
.
Similar calculation on lines AC and AB gives
 and
and  .
.
This shows that the distance of the point from the respective lines is linearly proportional to the original values
a,
b and
c.
[1]